El problema de Monty Hall
 El problema de Monty Hall es una de esas eternas curiosidades que se rehúsan a desaparecer en el olvido. No sólo es muy anti-intuitivo y lo sigue siendo aún luego de comprender correctamente la solución, sino que inspira las emociones más profundas. Cuando fue postulado en la columna Ask Marilyn (donde los lectores de la revista Parade podían hacerle preguntas a la mujer con el Coeficiente Intelectual más alto del mundo) causó un revuelo entre sus admiradores e incluso matemáticos profesionales la criticaron por su respuesta (correcta). Voy a resumir el problema para los que no conocen. Los demás pueden hacer dibujos en sus cuadernos hasta que termine.
El problema de Monty Hall es una de esas eternas curiosidades que se rehúsan a desaparecer en el olvido. No sólo es muy anti-intuitivo y lo sigue siendo aún luego de comprender correctamente la solución, sino que inspira las emociones más profundas. Cuando fue postulado en la columna Ask Marilyn (donde los lectores de la revista Parade podían hacerle preguntas a la mujer con el Coeficiente Intelectual más alto del mundo) causó un revuelo entre sus admiradores e incluso matemáticos profesionales la criticaron por su respuesta (correcta). Voy a resumir el problema para los que no conocen. Los demás pueden hacer dibujos en sus cuadernos hasta que termine.
Resulta que estamos en un programa de televisión en el que el participante tiene 3 puertas para elegir. Detrás de una de ellas hay un auto, mientras que las otras esconden dos cabras. A menos que seamos amantes de las cabras, probablemente prefiramos ganarnos el auto. Luego de decidirnos por una de las puertas, el presentador (que para los estadounidenses se llama Monty Hall pero los argentinos podemos llamarlo Dady Brieva) para dar un toque de dramatismo abre una de las dos restantes que él sabe contiene una cabra y nos ofrece cambiar nuestra elección anterior. ¿Qué nos conviene hacer?
Si nos atenemos al sentido común, parece ser una pregunta con poco sentido. Las probabilidades de que el auto esté detrás de la puerta que hayamos elegido o de la otra no deberían cambiar por el sólo hecho de que Dady Monty Hall haya abierto una puerta. Si antes eran de 1/3, ahora también lo son. Otro razonamiento parecido podría hacernos pensar que, ya que ahora hay dos puertas, las probabilidades son 50% de que el auto se encuentre detrás de alguna de ellas. En cualquier caso, uno podría pensar que da lo mismo si cambio o no y decidir quedarse con su elección original. Por desgracia para el participante que piense de esa manera, va a volverse caminando con más frecuencia que quién decida cambiar.
¿Cómo podría cambiar las probabilidades previas el mero hecho de descubrir el contenido de otra puerta? Simple: el presentador no abre una puerta al azar, por lo que al abrir una puerta, Monty nos está dando información adicional.
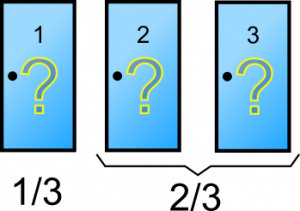
Al principio del juego existe 1/3 de probabilidad de que hayamos elegido la puerta correcta. Esto significa que, tomadas en su conjunto, hay un 2/3 de que el premio esté en alguna de las dos otras puertas. Tanto la matemática como el sentido común nos dicen que si nos dieran a elegir entre quedarnos con nuestra puerta o elegir el conjunto de las otras dos, es preferible lo segundo.
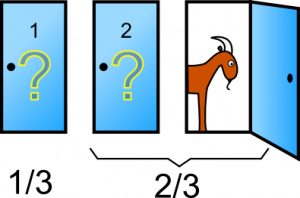
A continuación Monty abre una de ellas y nos propone elegir entre la original y la que queda. ¡Efectivamente lo que nos está proponiendo es el caso descrito anteriormente! Sabemos que hay 2/3 de probabilidad de que el premio esté detrás de la puerta 2 ó 3. También sabemos que existe un 0% de probabilidad de que éste esté detrás de la puerta 3 (porque Monty sólo puede abrir una puerta con una cabra). Por lo tanto, el 2/3 ahora se «concentró» en la puerta 2. Nos conviene cambiar.
Si son como yo, aún luego de entender intelectualmente el problema les quedará una sensación visceral de incredulidad. No hay mucho que hacer: la probabilidad no es intuitiva. Una razón más para ser escépticos y desconfiar, principalmente, del juicio propio.

Es indistinto cambiar la puerta elegida.
Ten en cuenta este detalle: el animador del programa abre una de las 2 puertas, a sabiendas de que allí hay una cabra. Por lo tanto, todo el análisis de probabilidades que has realizado, ya no corresponde hacerlo.
No hay elecciones al azar en este problema. Por lo tanto, no corresponde usar el cálculo de probabilidades.
Al principio, la probabilidad de acertar es 1/3.
Luego, el animador abre una de las 2 puertas, PERO SABIENDO
Miralo de esta otra forma:
Al principio, elegís una de las puertas. La probabilidad de acertar es 1/3.
Por otro lado, la probabilidad de que el auto esté en cualquiera de las otras 2 puertas es 2/3.
Ahora… hay un solo auto; por lo tanto en alguna de las 2 puertas que no elegiste, seguro que hay una cabra.
El animador del programa abre una de esas 2 puertas, sabiendo que en ella hay una cabra.
Pero ese nuevo dato a vos no te agrega nada: en una de las 2 puertas seguro que hay una cabra ¿de qué me sirve que el animador me diga en cuál está? No por eso va a ser más probable que en la otra haya un auto.
Mejor no darle más vueltas. Este es el resultado de una simulación de 30 juegos de Monty Hall cambiando de puerta y 30 sin cambiar. El resultado (empírico) es más que evidente:
Es matemática, conviene cambiar. También se pueden encontrar simuladores para que uno elija lo que quiere hacer. Sólo basta con buscar «monty hall simulator» en google.
Es obvio que nadie dice que las elecciones sean al azar. Lo que es al azar es como se distribuyen las cabras y los autos en las puertas.
Lo que llamas «calculo de probabilidades» sigue valiendo perfectamente cuando se revela lo que hay detras de una puerta. Es lo que se llama probabilidad condicional, que para este tipo de situacion consiste en calcular la probabilidad del evento «hay un auto detras de la puerta X» en un subconjunto del espacio muestral original.
Como dice Daneel, no hay que darle mas vueltas al asunto. Esta mas que claro entendiendo lo basico de teoria de probabilidad.
Si lo que te confunde es que la probabilidad «cambia» luego de que el animador toma una decision, no lo veas de esa manera (a mi no me gusta esa nocion de probabilidad). La probabilidad existe a priori y no cambia (siempre que sea el mismo juego). De hecho, decir que es indistinto cambiar la puerta equivale a decir que la probabilidad condicional de A (:= «el auto esta en la puerta 1») dado B (:= «hay una cabra en la puerta 2 o 3») es 1/2, mientras que uno sabe que la probabilidad de A es 1/3. Pero como A y B son eventos independientes se llega a un absurdo (1/2 != 1/3).