El problema de Monty Hall
 El problema de Monty Hall es una de esas eternas curiosidades que se rehúsan a desaparecer en el olvido. No sólo es muy anti-intuitivo y lo sigue siendo aún luego de comprender correctamente la solución, sino que inspira las emociones más profundas. Cuando fue postulado en la columna Ask Marilyn (donde los lectores de la revista Parade podían hacerle preguntas a la mujer con el Coeficiente Intelectual más alto del mundo) causó un revuelo entre sus admiradores e incluso matemáticos profesionales la criticaron por su respuesta (correcta). Voy a resumir el problema para los que no conocen. Los demás pueden hacer dibujos en sus cuadernos hasta que termine.
El problema de Monty Hall es una de esas eternas curiosidades que se rehúsan a desaparecer en el olvido. No sólo es muy anti-intuitivo y lo sigue siendo aún luego de comprender correctamente la solución, sino que inspira las emociones más profundas. Cuando fue postulado en la columna Ask Marilyn (donde los lectores de la revista Parade podían hacerle preguntas a la mujer con el Coeficiente Intelectual más alto del mundo) causó un revuelo entre sus admiradores e incluso matemáticos profesionales la criticaron por su respuesta (correcta). Voy a resumir el problema para los que no conocen. Los demás pueden hacer dibujos en sus cuadernos hasta que termine.
Resulta que estamos en un programa de televisión en el que el participante tiene 3 puertas para elegir. Detrás de una de ellas hay un auto, mientras que las otras esconden dos cabras. A menos que seamos amantes de las cabras, probablemente prefiramos ganarnos el auto. Luego de decidirnos por una de las puertas, el presentador (que para los estadounidenses se llama Monty Hall pero los argentinos podemos llamarlo Dady Brieva) para dar un toque de dramatismo abre una de las dos restantes que él sabe contiene una cabra y nos ofrece cambiar nuestra elección anterior. ¿Qué nos conviene hacer?
Si nos atenemos al sentido común, parece ser una pregunta con poco sentido. Las probabilidades de que el auto esté detrás de la puerta que hayamos elegido o de la otra no deberían cambiar por el sólo hecho de que Dady Monty Hall haya abierto una puerta. Si antes eran de 1/3, ahora también lo son. Otro razonamiento parecido podría hacernos pensar que, ya que ahora hay dos puertas, las probabilidades son 50% de que el auto se encuentre detrás de alguna de ellas. En cualquier caso, uno podría pensar que da lo mismo si cambio o no y decidir quedarse con su elección original. Por desgracia para el participante que piense de esa manera, va a volverse caminando con más frecuencia que quién decida cambiar.
¿Cómo podría cambiar las probabilidades previas el mero hecho de descubrir el contenido de otra puerta? Simple: el presentador no abre una puerta al azar, por lo que al abrir una puerta, Monty nos está dando información adicional.
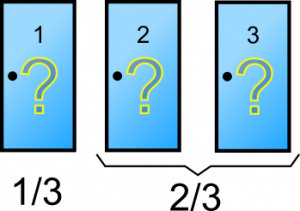
Al principio del juego existe 1/3 de probabilidad de que hayamos elegido la puerta correcta. Esto significa que, tomadas en su conjunto, hay un 2/3 de que el premio esté en alguna de las dos otras puertas. Tanto la matemática como el sentido común nos dicen que si nos dieran a elegir entre quedarnos con nuestra puerta o elegir el conjunto de las otras dos, es preferible lo segundo.
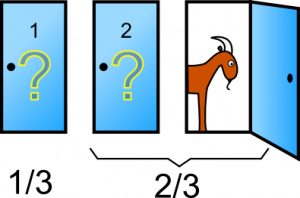
A continuación Monty abre una de ellas y nos propone elegir entre la original y la que queda. ¡Efectivamente lo que nos está proponiendo es el caso descrito anteriormente! Sabemos que hay 2/3 de probabilidad de que el premio esté detrás de la puerta 2 ó 3. También sabemos que existe un 0% de probabilidad de que éste esté detrás de la puerta 3 (porque Monty sólo puede abrir una puerta con una cabra). Por lo tanto, el 2/3 ahora se «concentró» en la puerta 2. Nos conviene cambiar.
Si son como yo, aún luego de entender intelectualmente el problema les quedará una sensación visceral de incredulidad. No hay mucho que hacer: la probabilidad no es intuitiva. Una razón más para ser escépticos y desconfiar, principalmente, del juicio propio.

La verdad, tengo que confesar que no entendí nada.
La teoría de probabilidad dice que la prob. de acertarle a un evento entre una cantidad de N posibles (todos con igual chance de salir) es 1/N. Para el número de un dado es 1/6, para un número en la ruleta es 1/37, y así.
Cuando uno tiene una información adicional sobre el evento al que está «apostando», entonces la probabilidad cambia. Se llama prob. condicional, porque hay una condición extra que influye en el resultado.
Este tipo de probabilidades tienen fórmulas bien precisas.
La prob. «sin información» se llama «inicial» y la prob. «con información extra» se llama «final».
La prob. inicial de acertarle al auto es 1/3.
Cuando el presentador abre una de las puertas, la cual es una cabra, la prob. de acertarle al auto aumenta a 1/2.
Sin embargo, el juego esconde un truco, y es que el presentador no da vuelta cualquier puerta, sino que «primero el participante ha elegido una puerta», y luego «el presentador abre una de las que el participante no eligió».
Eso termina influyendo en todo el proceso, ya que ahora los eventos inicial y final interactúan entre sí de otra manera, están ligados.
Así que el cálculo de la probabilidad debe ajustarse.
Se supone que la teoría de probabilidad asigna idéntica probabilidad a eventos de los cuales no se tiene ninguna información adicional.
Si bien parece que el jugador no tiene ninguna información sobre el «sistema», resulta que ha «influido» sobre él al elegir una de las puertas, porque el presentador no está capacitado para dar vuelta cualquiera de las puertas ahora. Está «condicionado», y entonces eso se devuelve al jugador como una nueva «información» adicional.
Supongamos que el auto está en la puerta 1.
Si el jugador elige la puerta 1, entonces el presentador está en libertad de elegir cualquiera de las 2 cabras, y no ha pasado nada, no se ha ganado nueva información.
Pero si justo el jugador eligió una de las cabras, el presentador está «obligado» a elegir la cabra restante para dar vuelta.
Esto reduce las posibilidades del juego, y por ende aumenta las probabilidades.
Uno tendría que analizar todos los eventos posibles, con sus probabilidades por separado, y se convencería.
A mí se me ocurre esta manera de modelar el «espacio muestral», como una colección de procesos de 4 etapas:
(A, E, P, F),
donde A = 1, 2 ó 3 es la puerta donde se ha colocado el auto,
E = 1, 2 ó 3 es la 1er. puerta elegida por el jugador,
P = 1, 2 ó 3 es la puerta que da vuelta el presentador,
F = 1, 2 ó 3 es la puerta que finalmente elige el jugador.
Hay casos que tienen prob. nula, por ejemplo si E = P ó P = F.
Hay casos que tienen prob. 1/36 (cuando E1 se elige igual a A),
y los demás casos tienen prob. 1/18 (cuando E1 se elige como una cabra).
La estrategia de «cambiar de puerta» dará más chances favorables al sumar todos los casos posibles.
Uno puede comparar con un juego parecido pero distinto, en que el jugador no elige ninguna puerta, y el presentador da vuelta una de las cabras.
Ahí es distinto, porque el presentador no está condicionado de ninguna manera a elegir una cabra u otra.
Y es equivalente a que de entrada te pongan sólo dos puertas, y que elijas una de las dos.
Pero como el jugador interactúa produciendo una cierta información… el juego cambia.
Recuerdo que hace tiempo lo entendí con Paenza… ahora cuando lo vi dije ¿a ver por qué era mejor cambiar?» ¡y no lo entendí! No puedo entenderlo ahora, intentaré mañana más lúcido, se que es una estupidez.
Famoso el problema dividio a la sociedad estadounidense, incluso, debido a la gran polemica desatada, le pidieron a un conocido matematico que opine y se equivoco, diciendo que luego de abierta la puerta tenía un 50% de probabilidades y como ya se explico, no es asi, luego debio retarctarse publicamente. Conclusion, cambiar de puerta aumenta las probabilidades.
…ya lo recuerdo el famoso matemático, entre muchos, que metió la pata era Paul Erdos. Me quede pensando… En el libro de la biografía de Paul Erdos, “El hombre que solo amaba a los numeros» (Pag 229 * donde esta la cabra? ) que lo recomiendo enormemente, Cuentan la historia como uno de los más famosos errores ed uno de los mas grandes matemáticos, Erdos.
Marilyn vos Savant, con se quien inicio el problema, según el guinnes de los records ostenta el record de ser la persona con mayor coeficiente (228). Es famosa por que ha hecho mucho dinero al igual que su esposo que invento un corazón artificial, pero es fashion y la comunidad científica la odia. Usa un anillo de bodas de carbón pirolitico, material usado por su marido para fabricar ese famoso corazón. Desde hace muchos años tiene una columna en una revista en donde invita a los lectores que le hagan preguntas. Este es su web site en el que podrán hallar un foro: http://www.marilynvossavant.com/
Yo lo tuve que releer un par de veces para terminar de entender.
Voy a plantear el problema de otra forma distinta. Tenés 3 puertas, en 1 hay un premio y en las otras dos no. Pudiendo elegir solamente una puerta, tenes 1/3 de posibilidades de acertar. ¿Y si pudieras elegir 2 puertas? Si el presentador del programa nos dejara por ejemplo, elegir las puertas A y C y descartar la B, tendríamos más chances de haber capturado el premio (2/3 de chances de haber atrapado el premio) que de solamente haber elegido una puerta al azar. Entonces el presentador de repente nos revela que en la puerta C que habías escogido no hay ningún premio, y nos da la opción de elegir entre la A y la B ¿Es más probable que este en la puerta A o en la B? Es más probable que este en la A, porque con las puertas A y C teníamos 2/3 tercios de que el premio estuviera allí, mientras que en la B solo había 1/3 de probabilidades. Como en la puerta C no hay nada, las probabilidades de que el premio este en A acaban de aumentar. Había 2/3 de probabilidades de haber atrapado el premio con A o C, si en C no hay nada las posibilidades de haber atrapado el premio se concentraron en A.
Lo mismo pasa en el problema planteado originalmente, solamente que en lugar de hacerte elegir dos puertas, ese conjunto de dos puertas se crea al haber uno elegido una única puerta. Si elegís la puerta A, hay 2/3 de posibilidades de que este en B o en C. Si nos aportan el dato de que en C no hay nada, las probabilidades de haber atrapado el premio recaen en la puerta B.
Ojalá haya ayudado a simplificar la comprensión del problema.
Yo nunca entendi por que fue tan controversial este problema. A mi me parece bastante mas anti-intuitivo creer que la Tierra es redonda (y no plana, como la percibimos) o que la materia esta hecha de particulas diminutas que interactuan entre si. Es decir, para creer en ello se requiere evidencia y una mayor fundamentacion que la que se necesita para el problema de Monty Hall.
Que buen problema! me parece que yo también lo había visto a Paenza plantearlo, y tampoco me había quedado muy en claro… ahora no es que estoy 100% seguro (es más, estoy 2/3 seguro :D), pero me quedó más claro al releer un par de veces el post y los comentarios… mañana lo tiro en el almuerzo laboral.
Es genial para almuerzos y reuniones de amigos; especialmente si hay alguno medio terco que te lo discute
Gracias saibaba y ryomashi por la explicación. Ahora lo entendí un poco más. Aunque hay algo que me sigue diciendo que está mal
Muy bueno. Lo explican en un episodio de numb3rs, serie interesante si les gustan este tipo de cosas.
Estuve pensando el problema de nuevo.
Si en vez de pensar la probabilidad que tengo de que el auto este en la puerta que elegí primero, lo pienso como la probabilidad de que en las otras dos puertas restantes haya 2 cabras parece tener más sentido. O sea, yo tengo las siguientes combinaciones:
Cabras en 1 y 2.
Cabras en 1 y 3.
Cabras en 2 y 3.
O sea, si yo elijo la puerta 1, solo hay 1/3 de probabilidades de que en 2 y en 3 haya cabras y, por ende, 2/3 de probabilidades de que haya una cabra en la puerta que elegí primero.
¿Está bien esto o estoy diciendo cualquier cosa?
Esta bien… pero no alcanza para explicar por que conviene cambiar de puerta despues. Lo que vos planteas es algo que vale siempre en el problema como esta planteado en la etapa inicial (antes de revelar el contenido de una puerta). O sea, inicialmente, eligiendo cualquier puerta la probabilidad de que haya un auto es de 1/3 y la de que haya una cabra es de 2/3. El problema es calcular la probabilidad de que haya una cabra o un auto detras de cada puerta luego de que se revele una.
PD: Detras de cada puerta, tiene que haber un auto o una cabra, por lo que siempre va a valer que la suma de la probabilidad de que haya un auto mas la de que haya una cabra es 1.
Si elegís la puerta 1, la prob. de que en esa puerta esté el auto es 1/3.
El juego que estás jugando es sólo esto: «acertarle al auto al primer intento».
La probabilidad que estás tratando de calcular es la de que en la puerta 1 haya un auto o una cabra.
Si elegís la puerta 1, y todavía no la dieron vuelta, ¿qué probabilidad hay de que haya un auto ahí?
Si repetís ese experimento muchas veces, ¿en qué proporción vas a acertarle al auto?
El juego de Monty Hall es distinto a esto de «acertarle a la primera».
Tiene más de una etapa.
El espacio muestral hay que armarlo teniendo en cuenta todo el proceso.
Por eso lo puse en 4 etapas, para que al menos se vea claro eso.
En el proceso intervienen 3 elecciones «al azar», dos del jugador y una del presentador, y no una sola del jugador.
La prob. calculada tiene que ser un «producto» de estas 3 cosas.
Y se puede agregar una 4ta, que es la elección de dónde poner el auto antes de comenzar el juego.
La clave está en que en el momento en que el presentador hace su elección… no es tan al azar. Está forzado o restringido en sus opciones.
Si señor , esa es la clave grande saibaba sos mas genio que la savant esa
Si, eso creo que lo entendí. Pero si yo lo planteo así, tratando de embocarle a las 2 cabras en lugar de al auto, no es lo mismo? O sea, si yo digo que hay una probabilidad de 1/3 de que en 2 y 3 haya cabras al mismo tiempo, yo ya se que en una de las puertas va a tener que haber una cabra, porque son 2 cabras y 3 puertas, entonces la probabilidad se concentra en la puerta que no abrí de ese par. Supongamos que abrí la puerta 3, queda la 2 por abrir. Por lo tanto si tengo 1/3 de probabilidades de que en la puerta 2 haya una cabra, hay 2/3 de probabilidades que no la haya, entonces que ahí hay mas probabilidades de que se encuentre el auto.
¿Por que el presentador va a tener una eleccion al azar? Al tipo le queda la opción de abrir 2 puertas, de las cuales una si o si tiene que tener a la cabra porque hay 3 puertas y 2 cabras. Si el tipo solo puede abrir las puertas que tienen cabras, no tiene mucha eleccion que digamos. A menos que las dos puertas tengan una cabra. O sea que su posibilidad de elegir queda relegada solo al caso en que el jugador haya elegido la puerta correcta, no?
Me parece que me convertí en la terca que discute
Cuando el jugador elige el auto, el presentador tiene 2 opciones.
En otro caso es como vos decís: tiene una sola opción.
Hay que considerar ambos casos para calcular las probabilidades del proceso.
En el caso de haber dos opciones, cada posibilidad se ha de multiplicar por 1/2, que es la prob. de que el presentador elija una cabra o la otra.
Cuando está forzado a elegir una sola puerte, ahí se multiplica por «1», porque sólo hay una elección posible…
Como sea, 1/2 y 1 son números distintos, y esto da números distintos en cada situación: dependen de la elección inicial del jugador.
Las probabilidades en un proceso de sucesivos eventos se calculan por la regla de multiplicación.
Hay que multiplicar la prob. de que «el auto esté en la puerta 1» por la prob. de que «el jugador elija la puerta 1» por la prob. de que «el presentador de vuelta la puerta 2» por la prob. de que «el jugador cambie de puerta».
La primer probabilidad es siempre 1/3,
la segunda también es 1/3,
la prob. de que el presentador elija la puerta 2 no es siempre la misma, depende de lo que pasó en los dos pasos anteriores (en qué puerta estaba el auto y si el jugador eligió o no esa puerta), así que ahí este número varía en dos casos, que deben analizarse por separado, y luego sumarse: hay el caso en que puede elegir, y ahí la prob. es 1/2, y el caso en que el presentador está forzado… la prob. es 1.
la prob. de que el jugador cambie de puerta es 1/2.
Hasta ahí es la etapa de modelado o descripción del espacio muestral con sus correspondientes probabilidades de cada evento posible.
Eso permite analizar todas las posibilidades, una por una.
Ahora bien, la «probabilidad de ganar», es un «evento particular» que consiste en reunir muchos pequeños eventos posibles: sólo aquellos que son «favorables»,
lo que requiere analizar todos los casos, quedarse con los «favorables» y luego «sumar sus probabilidades».
Cuántas cuentas hay que hacer depende de cómo se confeccionó el espacio muestral.
O sea, cómo armar «todas las situaciones posibles», y asignar una correcta probabilidad a cada una de ellas.
Según Ryomashi, hay un modo más breve que el mío.
Pero en cualquier caso, la prob. de ganar tiene que dar el mismo resultado.
Por ejemplo, al tirar dos dados, las probabilidades de cada número en cada dado es 1/6.
Para saber la prob. de una salida específica de un par de números en los dados, hay que multiplicar, y da 1/36.
Eso define el «espacio muestral».
Ahora, cosa aparte, viene definir «el juego», o sea, definir «el eveto de ganar».
Si el juego consiste en sacar 10 en la suma de los dados, entonces los «eventos favorables del espacio muestral» serían estos: (5; 5), (6; 4), (4; 6).
No hay más casos «favorables».
Cada uno tiene prob. 1/36.
La prob. de «ganar» es ahora la suma de cada uno: 1/36 + 1/36 + 1/36 = 1/12.
Si, eso esta bien. Aunque podes hacer el mismo razonamiento, ahorrandote el paso final, si en vez de considerar que la probabilidad de que hayan 2 cabras en 2 y 3 es 1/3 directamente consideras que la probalidad de que el auto este en 2 o en 3 es de 2/3. Pero vale igual .
O sea, la probabilidad de ganar en este caso me queda así:
Probabilidad de que el auto esté en la puerta 1 x probabilidad de que el jugador elija la puerta 1 x probabilidad de que el presentador de vuelta la puerta 2 x probabilidad de que el jugador cambie de puerta
Caso en que el presentador puede elegir= 1/3 x 1/3 x 1/2 x 1/2 = 1/36
Caso en que el presentador está forzado= 1/3 x 1/3 x 1/2 = 1/18
1/36 + 1/18= 1/12
¿Esta bien esto?
Si pero de esta manera, aunque sea mas larga, me ayuda a entender porque conviene cambiar de puerta.
Mejor que me siga dedicando a los bichos….
Pienso que la primer parte de las probabilidades caso por caso están bien.
Pero la probabilidad de ganar requiere otro tipo de análisis.
No quiero complicar la cosa más de lo que ya lo hice, pero aparece una probabilidad «condicional» en esto… (al final del post digo algo).
Lo que hay que sumar son todas las situaciones «favorables al jugador» que pueden darse,
considerando todas las combinaciones de autos y elecciones de puertas, que son estas:
* Con prob. 1/36: (1, 1, 2, 1), (1, 1, 3, 1), (2, 2, 1, 2), (2, 2, 3, 2), (3, 3, 1, 3), (3, 3, 2, 3).
* Con prob. 1/18: (1, 2, 3, 1), (1, 3, 2, 1), (2, 1, 3, 2), (2, 3, 1, 2), (3, 1, 2, 3), (3, 2, 1, 3).
Para saber la prob. de ganar «a secas», sale de sumar todo eso y da: 6×1/36 + 6×1/18 = 18/36 = 1/2.
Pero lo que pregunta el enunciado es «cuál es la mejor estrategia«.
Si interesa saber la prob. de ganar «en los casos en que se va a cambiar de puerta«, entonces eso corresponde a la lista de los últimos seis casos, con prob. 1/18, que da un total de 6/18 = 0.3333..
Pero la prob. de ganar «en los casos en que se va a mantener la misma puerta«, es la suma de los seis casos del primer renglón, que da: 6/36 = 0.16666…
O sea que para tener el doble de chances de ganar, conviene la estrategia de cambiar de puerta.
—————————–
El resultado final del problema como lo explica Daneel es distinto a los números que acabo de poner,
porque se requiere el concepto de «probabilidad condicional«.
Cuando se agrega una cierta «condición» hay que dividir por la «prob. de esa condición».
De la forma que he desmenuzado todo, me he terminado por marear a mí mismo,
y tengo dudas de cómo tomar la prob. condicional.
Pero a simple vista me parece correcto pensarlo así:
las condiciones de que el jugador «cambia de puerta» o «mantiene la misma puerta», tendrian prob. 1/2 cada uno.
Luego, divido por ese valor 1/2 cada una de las probabilidades que obtuve antes (6/18 y 6/36) y así obtengo el par de numeritos 2/3 y 1/3 que exhibe Daneel.
————
Hay muchas otras maneras de plantearlo… pero todas requieren usar alguna probabilidad condicional al final del procedimiento.
La manera que lo planteé es algo tediosa, pero tiene la ventaja de poder compararse con las probabilidades de juegos de dados, o de cartas, cuyas probabilidades uno puede analizar «a mano», sin meter nueva teoría, o justificaciones más «arriesgadas».
La demostracion con probabilidad condicional (sin enumerar casos) es simple (entendiendo lo que es probabilidad condicional):
Sean A el evento «el auto esta en la puerta 1» y B el evento «se muestra una cabra en 2 o en 3». Hay que calcular la probabilidad de A dado B ( P(A|B) ):
P(A|B) = P(B|A) * P(A) / P(B)
P(B) = 1 porque tiene que haber por lo menos una cabra en 2 o en 3, ya que hay 2 cabras y 3 puertas.
P(B|A) = 1 porque si hay un auto en 1, hay cabras en 2 y en 3 y, en particular, ocurre B.
Por lo tanto, P(A|B) = P(A) = 1/3
Enumerando casos seria:
Si elijo la puerta 1 y me muestran que en 2 o en 3 hay una cabra las posibilidades son:
(auto, cabra, cabra), (cabra, auto, cabra) o (cabra, cabra, auto)
Si uno se queda con la primera puerta, el unico caso favorable es (auto, cabra, cabra) y como hay 3 casos posibles, la probabilidad de que el auto este en 1 es 1/3.
Digo yo, a nadie se le ocurrió hacer un análisis empírico?
En una computadora sólo es necesario programar las etapas de juego, dejar que la PC elija al azar (de acuerdo a las limitaciones de cada etapa) y luego de ejecutarse, digamos unas 10.000 veces, ver los resultados.
Espero que alguien con conocimientos de programación se le haya ocurrido ya y este dando vueltas por la red. De ser así, alguno que conozca esto puede facilitar el link?
obviamente que se les ocurrió. Y seguramente encontrarás varios enlaces, por ejemplo, estos están en las referencias del artículo de wikipedia:
http://demonstrations.wolfram.com/MontyHallParadox/
http://www.nytimes.com/2008/04/08/science/08monty.html
http://www.stat.sc.edu/~west/javahtml/LetsMakeaDeal.html
http://www.shodor.org/interactivate/activities/SimpleMontyHall/
por cierto, en el segundo simulador, en el primer intento que hice, no hice el cambio… y gané el auto eso es lo que tienen las «probabilidades» y aplicar la teoría de grandes números a casos particulares.
El primer link era justo en lo que estaba interesado.
No se me había ocurrido lo de hacerlo interactivo, y funciona! (a baja escala, claro)
Gracias N3RI!
Hay otra forma de entenderlo mediante fuerza bruta: imaginen que en lugar de ser 3 puertas son un 1.000.000, y que luego de elegir el presentador abre las puertas mostrando 999.998 cabras.
Por cierto, muy buena tu explicación, Daneel. No se me había ocurrido verlo como poder elegir el conjunto de las 2 restantes.